Problem Statement
This test examines the long wave run-up on a sloping bottom. The problem is 1D and radially symmetric,
and we only look at a quarter of the domain, with one open boundary at the outer edge of
the domain. A linear bottom profile is chosen here and compared with analytical solution
given by Lynch and Gray (1978). It tests the
algorithms to solve the continuity equation as well as the advection.
Benchmark set-up
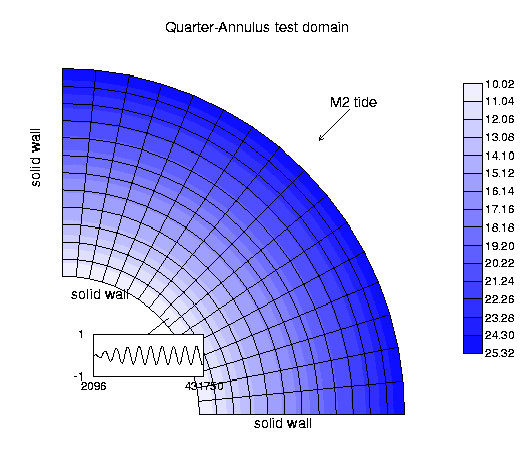
Domain: a quarter annulus with inner and outer radii of 60.96km and 152.4km, and a linear bottom slope, with depth varying from 10.02m at the inner radius to 25.05m at the outer radius. An M2 tide of 0.3048m amplitude is imposed at the open boundary.
Domain discretization: radially uniform discretization is used in the horizontal, and a 2D depth-averaged model (with only one vertical layer) is used in ELCIRC to facilitate the comparison.
Time: total simulation time is 5days, with dt=1047.936sec (300s for SELFE). The choice of dt will affect the numerical diffusion caused by the backtracking algorithm. A safe bet is to choose a dt such that the typical Courant number is on the order of 1.
Parameters:
Inviscid fluid is assume in order to compare with the analytical solution. Bottom friction, Corilois,
and horizontal diffusion are all neglected. The implicitness parameter (\alpha) is set to be 0.6,
as tests show that \alpha=0.5 (i.e., Crank-Nicholson scheme)
gives the best accuracy. We also imposed the analytical value of velocity at the boundary in the SELFE run
to bypass the problem of inflow condition in backtracking. This was found to slightly improve the phase error.
ELCIRC run
Input files
Results
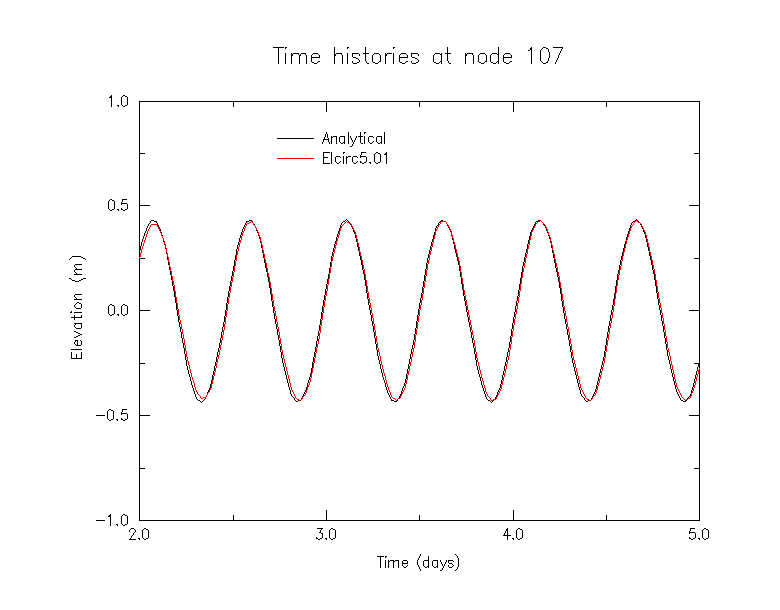
SELFE run
Input files
Results
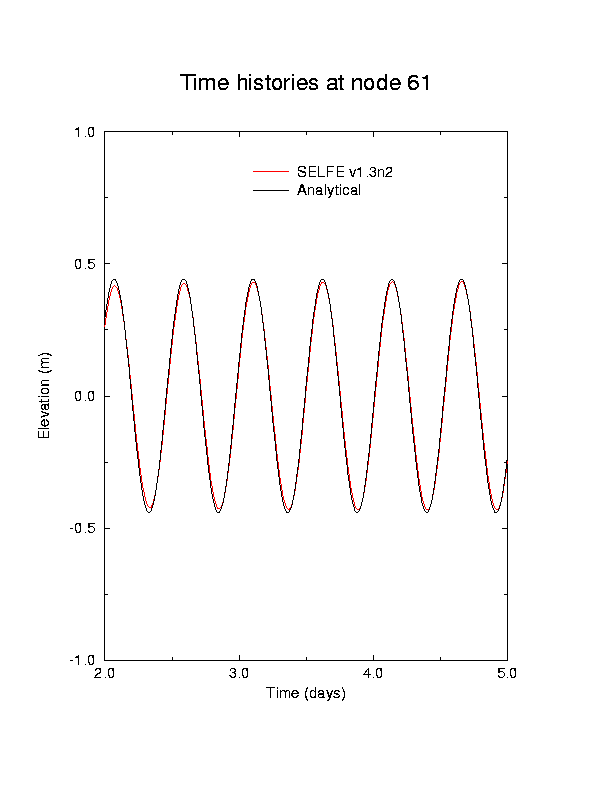
Discussion
References
Lynch DR and Gray WG. Analytical solutions for computer flow model testing. J. Hydraulics Division, 1978; 104: 1409-28.